| Basic
Principle |
 |
 |
The basis
vector method determines the optimal shape by combining
possible basic shape candidates (called basis vectors)
that the designer imagines for the original shape.
Each basis vector has its weight factor. Applying
weight factors change the shape of basis vectors.
The final optimal shape is represented as the union
(logical sum) of the basis vector with different weight
factors. |
|
 |
A basis vector
is sometimes indicated by acronym as "BV". In CLAY
OPERA, any number of basis vectors can be defined.
Therefore, usually a number is appended to each basis
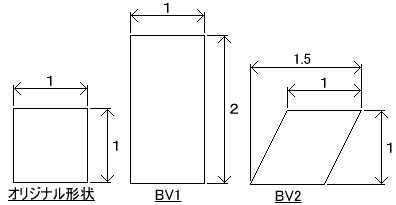
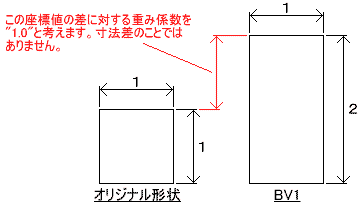
vector. Suppose we create two shapes (original and
basis) as shown in the above figure. In CLAY OPERA,
the initial value for the weight factor of the basis
vector is "1.0" when it is created. For example, BV1
is defined as follows: |
 |
|
 |
 |
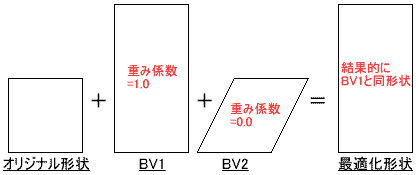
The optimal
shape can be defined by using a relationship represented
by the following formula:
Opt=Org+{(Org−BV1)*W1+(Org−BV2)*W2 . . . +(Org−BVn)*Wn} |
 |
Opt: Coordinate
of the optimal shape BV: Coordinate of the basis vector
Org: Coordinate of the original shape W: Weight factor
of the basis vector |
 |
The above
formula indicates that "the final optimal shape is
represented as the union (logical sum) of the basis
vector with different weight factors" as described
in above. For this relationship to be established,
there must be vertex coordinate data for the original
shape and basis vectors. This means that it is impossible
to change the element configuration (topology). This
is a distinctive feature of the basis vector method.
Since weight factors are signed, the vertex coordinates
could be inverted against the original shape.
The following figures show how the optimal shape changes
according to the weight factor of the basis vector.
|
 |
|
 |
|